TAM SAYILAR
TAM SAYILAR
Tamsayılar pozitif tam sayılar kümesi, negatif tam sayılar kümesi ve sıfırın birleşimi ile oluşan sayı kümesidir. Sayma sayılarının soluna artı anlamında + işareti yazıldığında +1, +2, +3, +4, ...sayıları elde edilir. Bu sayılara pozitif tam sayılar denir ve pozitif tam sayılar kümesi Z+ ile gösterilir. Sayma sayılarının soluna eksi anlamında işareti yazıldığında -1, -2, -3, -4, ... sayıların elde edilir. Bu sayılara negatif tam sayılar denir ve negatif tam sayılar kümesi Z- ile gösterilir. Pozitif tam sayılar, negatif tam sayılar ve sıfır, tam sayıları oluşturur ve tam sayılar kümesi Z ile gösterilir.
» Sıfır ne negatif ne de pozitif tam sayıdır. Sıfırın işareti yoktur.
» Solunda işareti olmayan (sıfır hariç) sayılar pozitif olarak alınır.
» Her doğal sayı aynı zamanda bir tam sayıdır.
Tam Sayıların Sayı Doğrusunda Gösterilmesi
Tam sayılar sayı doğrusu üzerinde gösterilirken; bir doğru üzerinde bir nokta alınıp sıfır sayısıyla eşlenir ve bu referans noktası olarak alınır. Sağında ve solunda eşit aralıklarla noktalar işaretlenir. Sıfır noktasının sağındaki noktalar sırasıyla +1, +2, +3, ... ile, solundaki noktalar sırasıyla -1, -2, -3, ... ile eşlenir. Aşağıdaki sayı doğrusunda A noktası -4, B noktası -2, C noktası +1, D noktası +3 ile eşlenmiştir. Bu noktalar ve görüntüleri aşağıdaki sayı doğrusunda verilmiştir.
MUTLAK DEĞER
Mutlak değer; sayı doğrusu üzerindeki herhangi bir sayının referans noktasına olan uzaklığını gösteren sayıya o sayının mutlak değeri denir. Bir sayının mutlak değeri, sayının birbirine paralel iki çizgi arasına yazılmasıyla gösterilir. Aşağıdaki örneklerde de görüldüğü üzere; pozitif veya negatif her tam sayı mutlak değer dışına pozitif olarak çıkar. Sıfırdan farklı her tam sayının mutlak değeri pozitif tam sayıdır.
I+42I= +42
I-12I = +12
I-8I = +8
TAM SAYILARIN KARŞILAŞTIRILMASI
» Sayı doğrusu üzerinde negatif tam sayılar sıfırın solunda, pozitif tam sayıları sıfırın sağındadır.
» Sıfır, bütün negatif tam sayılardan büyüktür. 0 > -1 > -55 > -99
» Sıfır, bütün pozitif tam sayılardan küçüktür. 0 < 5 < 42 < 78
» Sayı doğrusu üzerinde sağa doğru gidildikçe sayılar büyür, sola doğru gidildikçe sayılar küçülür.
» Pozitif tam sayılar sıfırdan uzaklaştıkça büyür. En küçük tam sayı +1 dir.
» Negatif tam sayılar sıfıra yaklaştıkça büyür. En büyük negatif tam sayı -1 dir.
» Negatif her tam sayı, pozitif her tam sayıdan küçüktür.
» Her tam sayı solundaki tüm tam sayılardan büyük, sağındaki tüm tam sayılardan küçüktür.
TAM SAYILARDA TOPLAMA İŞLEMİ
Tam sayılarda toplama işlemi yapılırken, verilen tam sayıların aynı veya farklı işaretli oluşlarına göre işlem yapılır.
Aynı İşaretli Tam Sayılarda Toplama İşlmemi
Aynı işaretli iki tam sayı toplanırken, sayıların mutlak değeri toplanır, sonuçta bulunan sayının soluna toplanan sayıların ortak işareti yazılır. Aşağıdaki örnekte verilen -7 ve -10 aynı işaretli tam sayılardır. Aynı işaretli oldukları için bu tam sayılar toplanır ve sonucun işareti ise ortak işaret olan (-) işaretidir.
Örnek 1 : (+5) + (+7) = +12
Örnek 2 : (-7) + (-10) = -17
Farklı İşaretli Tam Sayılarda Toplama İşlemi
Farklı işaretli tam sayılarda toplama işlemi yapılırken, sayıların mutlak değerleri bulunur. Bu değerlerin büyük olanından küçük olan çıkarılır. Elde edilen sayının soluna mutlak değerce büyük olan sayının işareti yazılır. Aşağıdaki örnekte verilen +4 ve -8 tam sayıları toplanırken, zıt işaretli oldukları için büyük sayıdan küçük sayıyı çıkarırız. Sonuca ise büyük sayının işaretini yazarız.
Örnek 1 : (+4) + (-8) = -4
Örnek 2 : (-10) + (+7) = -3
Herhangi bir sayının sıfır ile toplamı sayının kendisine eşittir.
0 + (-12) = -12
Mutlak değeri eşit ve ters işaretli iki tam sayının toplamı sıfırdır.
(+23)+(-23) = 0
İkiden fazla tam sayının toplamı bulunurken, aynı işaretli sayılar kendi aralarında toplandıktan sonra ters işaretli sayıların toplanması kolaylık sağlar.
Soru : (-12) + (+5) + (-8) + (+7) işleminin sonucunu bulunuz.
Çözüm : Aynı işaretli tam sayıları bir araya getirerek kendi aralarında toplarız. Daha sonra ise farklı işaretli iki tam sayı toplamı kuralından, birbirinden çıkararak büyük olan sayının işaretini sonuca ekleriz.
(-12) + (-8) + (+7) + (+5)
(-20) + (+12) = -8
Bir tam sayının toplama işlemine göre tersi
İki tam sayının toplamı sıfıra eşit ise bu sayılar toplama işlemine göre birbirinin tersidir. Negatif bir tam sayının toplama işlemine göre tersi pozitif, pozitif bir tam sayının toplama işlemine göre tersi negatif bir tam sayıdır. Sıfırın toplama işlemine göre tersi sıfırdır.
(+9) un toplama işlemine göre tersi (-9),
(-32) nin toplama işlemine göre tersi +32,
0 (sıfır) ın toplama işlemine göre tersi 0 (sıfır) dır.
Toplama İşleminin Sayı Doğrusunda Gösterilmesi
Tam sayılarda toplama işlemi sayı doğrusu üzerinde gösterilirken; eklenen sayı pozitif ise sayı doğrusu üzerinde sağa doğru, eklenene sayı negatif ise sola doğru ilerlenir. Yukarıda verdiğimiz örnekte verilen tam sayıların her ikisi de pozitif sayı olduğu için sağa doğru ilerleyerek sonucu +8 olarak bulduk. Örneğimiz (+3) + (-5) şeklinde olsaydı; ilk önce 3 birim sağa ilerleyerek +3' e gelirdik. Daha sonra beş birim sola doğru ilerlerdik (5 negatif olduğu için). Sonucu -2 olarak bulurduk.
Yukarıda verdiğimiz örnekte verilen tam sayıların her ikisi de pozitif sayı olduğu için sağa doğru ilerleyerek sonucu +8 olarak bulduk. Örneğimiz (+3) + (-5) şeklinde olsaydı; ilk önce 3 birim sağa ilerleyerek +3' e gelirdik. Daha sonra beş birim sola doğru ilerlerdik (5 negatif olduğu için). Sonucu -2 olarak bulurduk.
Tam Sayılarda Toplama İşlemi Özellikleri
» Kapalılık Özelliği
» Değişme Özelliği
» Birleşme Özelliği
» Etkisiz Eleman Özelliği
» Ters Eleman Özelliği
(+8) + (+4) = +12 örneğinde toplanan tam sayıların sonucu olan +12 bir tam sayıdır.
Değişme Özelliği: Tam sayılarda yapılan toplama işleminde terimlerin yerlerinin değişmesi sonucu değiştirmez.
(-4) + (-3) = -7
(-3) + (-4) = -7
Birleşme Özelliği: Tam sayılarda toplama işlemi yapılırken, terimler ikişer ikişer değişik biçimlerde gruplandırılarak toplanırsa sonuç değişmez.
[(+7) + (-5)] + (+8) = +10
(+7)+ [(-5) + (+8)] = +10
Yukarıda verilen örneklerde birinci işlemde ilk önce +7 ile -5 toplanarak +2 bulunur. Daha sonra +8 ile toplanarak +10 sonucu elde edilir. İkinci işlem de ise ilk önce -5 ve +8 toplanarak +3 sonucu elde edilir. Daha sonra +7 ile +3 toplanarak +10 sonucuna ulaşılır. Görüldüğü üzere toplama işleminde birleşme özelliği vardır.
Etkisiz Eleman Özelliği: Bir tam sayının sıfır (0) ile toplamı yine kendisine eşittir. Bu nedenle sıfır (0) toplama işleminin etkisiz elemanıdır.
Ters Eleman Özelliği: Mutlak değerleri eşit, işaretleri zıt olan iki tam sayı toplama işlemine göre birbirinin tersidir. (-5) ve (+5) tam sayılarının mutlak değerleri birbirine eşit ve işaretleri birbirinin tersi olduğu için bu sayılar birbirinin tersidir.
TAM SAYILARDA ÇIKARMA İŞLEMİ
Tam sayılarda çıkarma işlemi yapılırken; çıkanın işareti değiştirilir ve eksilen sayı ile toplanır. Aşağıdaki örneği inceleyiniz.
Örnek: (+6) - (-4) işleminin sonucunu bulalım.
Çözüm: İlk önce çıkan sayının işaretini değiştirelim. Eksilen sayımız olan -4 işaret değiştirerek +4 olacaktır ve bu tam sayılar arasındaki işlem toplamaya dönüşecektir. İfademizin yeni hali aşağıdaki gibidir.
(+6) + (+4)
Şimdi ise toplama işlemini yapalım. Aynı işaretli oldukları için toplayarak sonuca ortak işareti yazarız.
(+6) + (+4)= +10 olarak bulunur.
Tam sayılarda çıkarma işlemini modelleme ile yapalım. Aşağıdaki örnekte (-5) - (-3) işlemi modelleyerek yapılmıştır.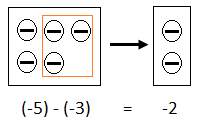
Çıkarma İşleminin Sayı Doğrusunda Gösterimi
Tam sayılarda çıkarma işlemini sayı doğrusu üzerinde gösterirken; ilk önce sıfırdan başlayarak eksilen sayıya ok çiziyoruz. Yukarıda verilen örnekte eksilen sayımız -7 dir. Bu nedenle ilk önce sıfırdan -7 ye ok çiziyoruz. Daha sonra çıkan sayımızın işaretini değiştiriyoruz. Örnekteki çıkan sayı -5 tir ve işareti değişince +5 olur. Şimdi ise pozitif sayılarda sağ tarafa ilerlediğimiz için -7 noktasından 5 birim sağa doğru ilerleyerek -2 noktasına ulaşıyoruz.
Tam sayılarda çıkarma işleminde değişme özelliği ve birleşme özelliği yoktur. Toplama işlemindeki gibi kapalılık özelliği ve etkisiz eleman özelliği vardır.
TAM SAYILARDA ÇARPMA İŞLEMİ
Tam sayılarda çarpma işlemi, terimleri aynı olan toplama işleminin kısa yoldan yapılışıdır. Örneğin; +5 +5 +5 +5 =20 işleminde 4 tane 5 toplanmıştır. Bu işlem kısaca 4 . 5 = 20 şeklinde de yapılabilir.
Tam sayılarla çarpma işleminde; Aynı işareti iki tam sayının çarpı pozitiftir. Farklı işaretli iki tam sayının çarpımı ise negatiftir. Aşağıdaki çarpma işlemi ile ilgili örnekleri inceleyiniz.

Tam sayılarda çarpma işlemi ile ilgili, yukarıda verilen örnekte 4 . 2 işlemi, 4 tane 2 nin toplamı demektir. Dört defa iki birim ilerlenerek 8 sonucuna ulaşılmıştır. Bu soruyu isterseniz 2 . 4 şeklinde de çizebilirsiniz. İki kere 4 birim ilerleyerek sonucu yine 8 olarak bulursunuz.
Sayma Pulları ile Modelleyerek ÇarpmaTam sayılarda çarpma işlemi sayma pulları ile modellenerek de yapılabilir. (+5) . (-2) işlemini sayma pulları ile modelleyerek çözelim. Bunun için 5 tane 2 li sıfır çifti bulunan bir modele, 5 tane 2 li (-) pulu eklenebilir. Aşağıdaki şekli inceleyiniz.

Çarpma İşleminin Özellikleri
Tam sayılarda çarpma işlemi değime özelliğine sahiptir. (-2) . (+3) işleminin sonucu ile (+3) . (-2) işleminin sonucu aynıdır. Tam sayılarda çarpma işleminde terimlerin yer değiştirmesi çarpımı değiştirmez.
Birleşme Özelliği: [(-2) . (+4)] . (+2) işlemi ile (-2) . [ (+4) . (+2) ] işleminin sonucu aynıdır. Her iki çarpma işleminde de sonuç (-16) olarak bulunur. Tam sayılarda çarpma işleminin birleşme özelliği vardır.
Yutan Eleman Özelliği: Bütün tam sayıların sıfır (0) ile çarpımı sıfırdır. Sıfır çarpma işleminde yutan elemandır.
Etkisiz Eleman Özelliği: Tam sayılarda yapılan çarpma işleminde bir (1) etkisiz elemandır. Bütün tam sayıların bir (1) ile çarpımı kendisine eşittir.
Dağılma Özelliği: Çarpma işleminin toplama ve çıkarma işlemleri üzerine dağılma özelliği vardır.
TAM SAYILARDA BÖLME İŞLEMİ
Tam sayılarla bölme işlemi yaparken dikkat etmemiz gereken en önemli nokta verilen tam sayıların işaretleridir. Verilen tam sayılar aynı işaretli ise; bölümün sonucu pozitiftir. Farklı işaretli iki tam sayının bölümü ise negatiftir.
Aynı işaretli iki tam sayı bölünürken sayıların mutlak değerleri bölünüp, bulunan sonucun soluna + işareti yazılır. Farklı işaretli iki tam sayı bölünürken sayıların mutlak değerleri bölünüp, bulunan sonucun soluna - işareti yazılır.

» Bir tam sayının +1 e bölümü, sayının kendisine eşittir.
» Bir tam sayının -1 e bölümü sayının toplama işlemine göre tersine eşittir.
» Bir tam sayının sıfıra bölümü tanımsızdır.
» Sıfırın bir tam sayıya (sıfır hariç) bölümü sıfırdır.
» Bir tam sayıyı 10 veya 10 un kuvvetleri ile bölerken bölünen tam sayının basamaklarından 10 un kuvvetinde bulunan sayı kadarı sağdan sola doğru sayılarak virgülle ayrılır. Eksik kalan basamaklar sıfır ile tamamlanır.
WWW.SANALOKULUMUZ.COM
Yorumlar - Yorum Yaz



